|
|
|
|
QisBool
Concepts |
|
|
|
|
|
|
|
|
|
|
Q1. What an instance of
QisBool ? |
|
1.
An instance of QisBool is a single QisBool object. 2.
A QisBool object is created using QisBool_Create and destroyed
using QisBool_Destroy. 3.
A QisBool object is identified by a unique handle
(void*) returned when QisBool_Create executes successfully. 4.
Almost all QisBool functions require this handle to be
passed as a parameter so that they know which instance of QisBool to operate
upon. 5.
Each instance of QisBool object requires 1 QIS BOOLEAN
license. 6.
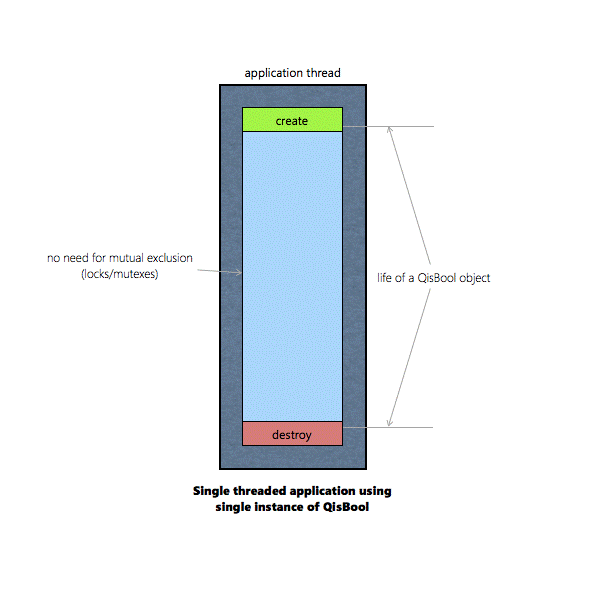
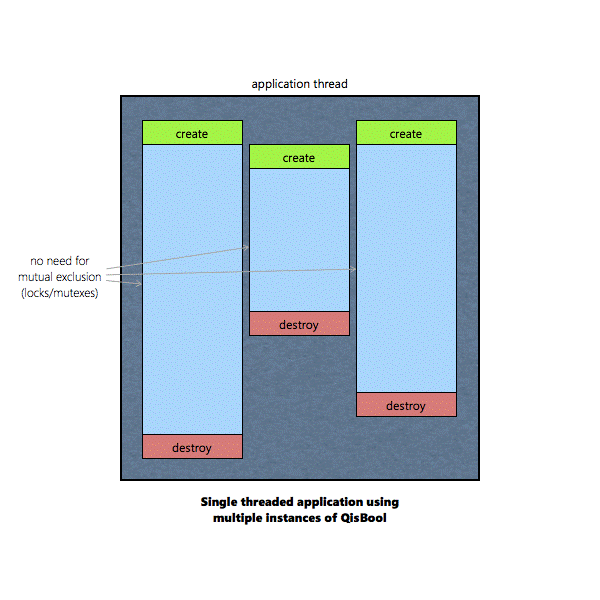
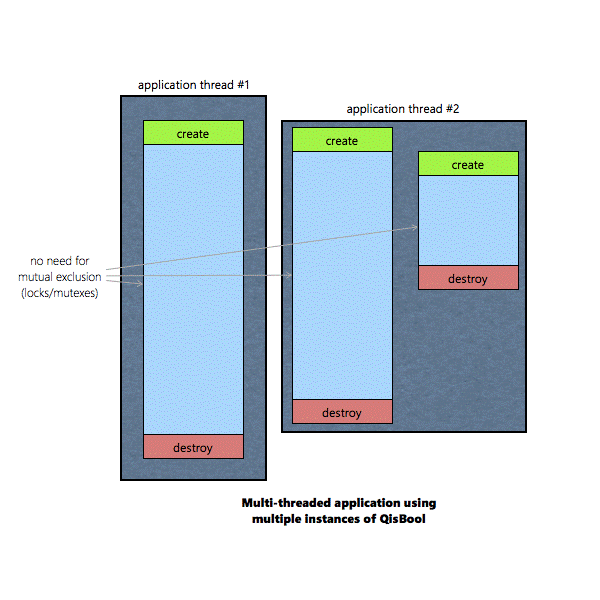
Multiple instances of QisBool objects can co-exist in
parallel. 7.
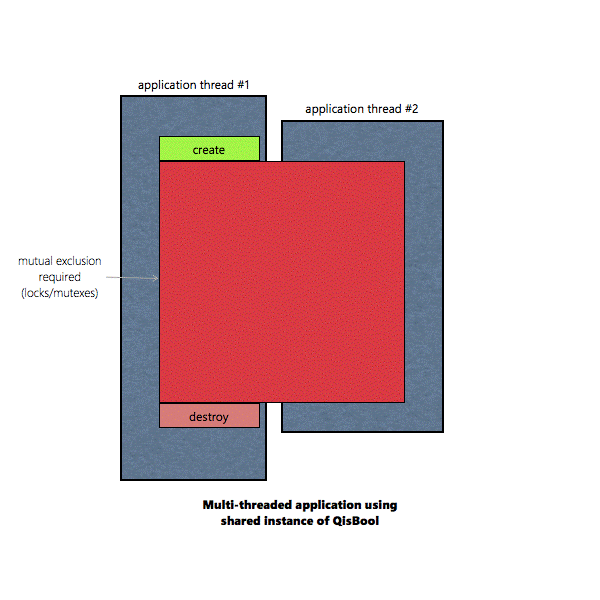
If an instance of QisBool is shared by two or more
threads, the QisBool functions operating on that instance must be protected
by mutual exclusion (locks/mutexes) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Q1. What are the units of
the geometric data used and generated by QisBool functions ? |
|
1.
QisBool functions do not conform to any units. 2.
All geometric data used and generated by QisBool
functions are represented by integers. 3.
It is the responsibility of the client code to convert
the input data to from their respective units to integers based on certain
acceptable 'resolution' (grid) and the re-convert the output back into the
client's units using the same resolution. 4.
For example, to convert the width of a path (0.5um) to
integers with a resolution of 0.001 (1000 grids per um or nm resolution), the
conversion would be applied as w = 0.5/0.001 = 500. The final width passed to
QisBool function would be 500. To convert a width (6578) generated by a
QisBool function back to the client's units with a resolution of 0.001,
w=6578*0.001 = 6.578um 5.
Similarly, to convert x,y co-ordinates of a point
(123.45um, 456.789um) to integers with a resolution of 0.001, the conversion
would be applied as x = 123.45/0.001 = 123450 and y = 456.789/0.001 = 456789.
The final co-ordinates passed to QisBool function would be (123450, 456789).
To convert an x,y co-ordinate (-890123, 7891) generated by a QisBool function
back to the client's units with a resolution of 0.001, x = -890123*0.001 =
-890.123 and y = 7891*0.001 = 7.891 i.e (-890.123um, 7.891um). 6.
Note: Certain QisBool
functions accept geometric parameters (such as sizing amount) as doubles.
This should not be confused with the units of the parameter. The geometric
value must be unit less (integer) even though it is passed as a double. If a
non-integral value is passed, it will be rounded off to the nearest integer
either before or after the computation. |
|
|
|
|
|
Q1. How does QisBool
represent polygons ? |
|
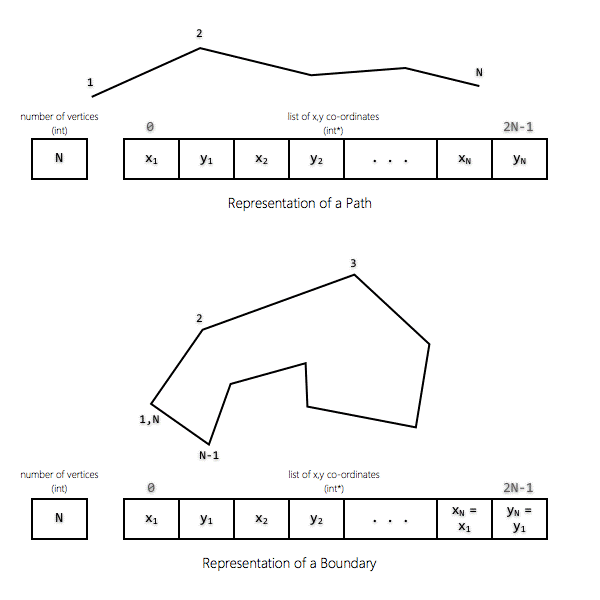
1.
QisBool represents polygons using TWO pieces of
information: 1.
Number of Vertices (int) (NV) 2.
List of x,y co-ordinates (int*) (XY) 2.
The number of vertices represents the number of points
in the polygon. If the polygon is open (such as a path), the last and the
first point are distinct. If the polygon is closed (such as a boundary), the
last and the first point have the same x,y values. Therefore, a rectangle has
5 vertices while a single segment path as 2 vertices. 3.
The list of x,y co-ordinates is an integer array of
(NV * 2) integers or NV x,y pairs. The 1st element of this array (index 0)
represents the x co-ordinate of the first vertex, the 2nd element of the array
(index 1) represents the y co-ordinate of the first point. Index 1 and 2
represent the second vertex and so on. 4.
The order in which the vertices appear in the list of
x,y co-ordinates determines whether it is 'clock-wise' or 'counter-clockwise' |
|
|
|
|
|
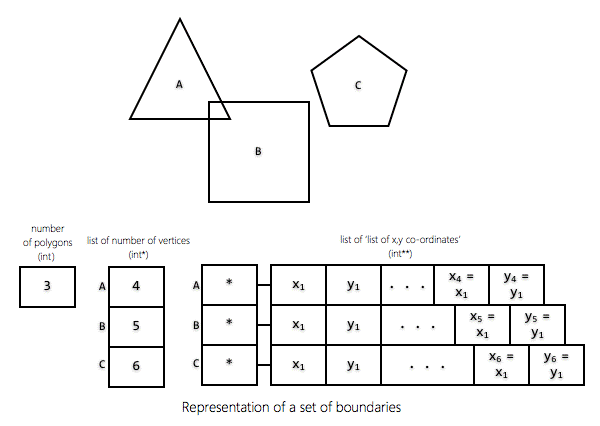
1.
To represent a SET of polygons, we need THREE pieces
of information: 1.
Number of polygons in the set (int) (N) 2.
A list of 'number of vertices' for each polygon in the set (int*) (NV) 3.
A list of 'list of x,y co-ordinates' for each polygon in the set (int**) (XY) 2.
NV is an array of N integers and XY is an array of N
integer arrays. If I is an index of a specific polygon in this set, then
NV[I] = number of vertices in that polygon and XY[I] = list of x,y co-ordinates
of that polygon. Note that number of integers in XY[I] = (NV[I] * 2) in
accordance with Q1 /Pt. 3 above. |
|
|
|
|
|
|
|
|
|
Q1. What is a Leonov polygon
? |
|
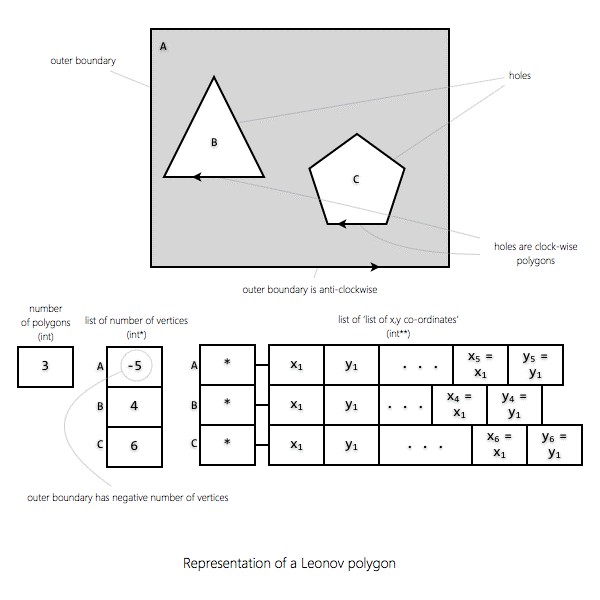
1.
A Leonov polygon is a polygon with holes. 2.
It consists of an 'outer boundary' and one or more
'holes' that lie completely inside (and do not intersect) the outer boundary.
|
|
|
|
Q2. How is a Leonov polygon
represented in QisBool ? |
|
1.
A Leonov polygon is represented in QisBool as a set of
polygons. 2.
The first polygon in this set represents the outer
boundary or the enclosing polygon while the remaining polygons represent the
holes. 3.
To differentiate the outer boundary from the holes and
to differentiate a leonov polygon from a regular polygon
set,
the number of vertices NV[0] for the outer boundary is negative (-1 * number
of vertices). 4.
Therefore, a Leonov polygon can be represented by
THREE pieces of information just like a regular polygon
set: 1.
Number of polygons (number of holes + outer polygon) (int) (N) 2.
List of 'number of vertices' for each of those polygons (int*) (NV) 3.
List of 'list of x,y co-ordinates' for each of those polygons (int**) (XY) 5.
NV[0] and XY[0] represent the outer boundary while
NV[1..N-1] and XY[1..N-1] represent the holes. 6.
NV[0] is negative. 7.
The only difference between the representations of
Leonov polygon and a set of regular polygons is that the
latter never contains a polygon with negative number of vertices. 8.
The orientation of the outer boundary is
counter-clockwise while the orientation of the holes is clock-wise. |
|
|
|
|
|
|
|
|
|
Q1. What are cutlines ? |
|
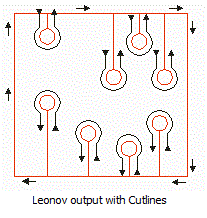
1.
Cutlines is one of the techniques used to convert a Leonov polygon into a regular
polygon. 2.
Cutlines are edges that join the boundary of a hole to
the outer boundary. 3.
A polygon with cutlines is a single re-entrant
polygon. |
|
|
|
|
|
|
|
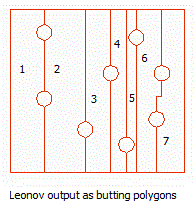
Q1. What are butting
polygons. |
|
1.
Butting polygons are polygons which have
one or more but not all edges that coincide. 2.
Butting is one of the techniques used to
convert a leonov polygon into regular
polygons without using cutlines. |
|
|
|
|
|
|
|
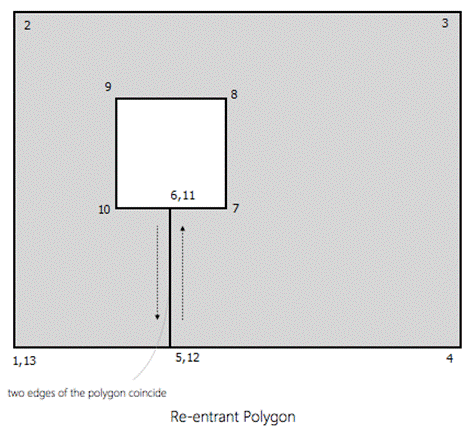
Q1. What are re-entrant
polygons ?. |
|
1.
Re-entrant polygons are polygons in which
at least two edges coincide. 2.
A polygon generated by using cutlines on a leonov polygon is re-entrant. |
|
|
|
|
|
|
|
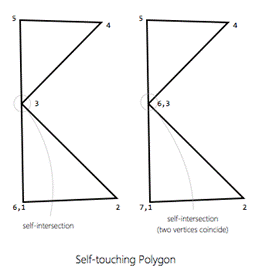
Q1. What are self-touching
polygons ?. |
|
1.
Self touching polygons are polygons where
either two vertices (except the first & last) coincide or a vertex lies
on an edge not originating/ending on that vertex. |
|
|
|
|
|
|
|
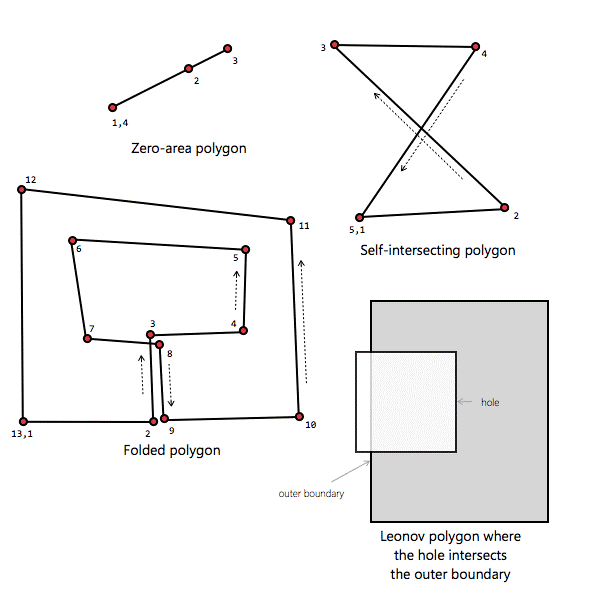
Q1. What kinds of polygons
should be avoided being used as input to QisBool functions ?. |
|
1.
An open boundary (where the first vertex
is not the same as the last) unless it is a path. 2.
A polygon with zero area. (a point) 3.
A one-dimensional polygon (0 width/height)
unless it is a path (a line) 4.
A leonov polygon where the hole crosses
the outer boundary. 7.
Self-intersecting polygons |
|
|
|
|
|
|
|
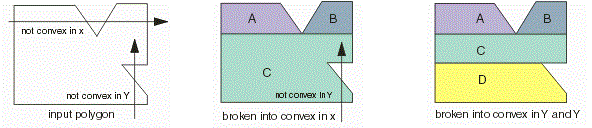
Q1. Which polygon is convex
in X ? |
|
1.
A polygon is convex in X if there is no
line parallel to X that intersects the polygon edges at more than TWO points. |
|
|
|
Q2. Which polygon is convex
in Y ? |
|
1.
A polygon is convex in X if there is no
line parallel to Y that intersects the polygon edges at more than TWO points. |
|
|
|
Q3. Which polygon is convex
in X and Y (Fully Convex) ? |
|
1.
A polygon is fully convex if there is no
line that intersects the polygon edges at more than TWO points. |
|
|
|
|
|
|
|
Q1. What is standard sizing
? |
|
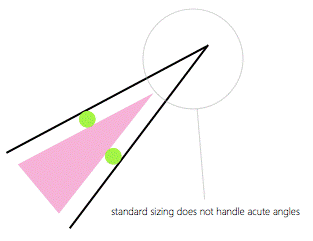
1.
Standard sizing is a technique that
applies sizing to a polygon by generating new edges that are at constant
distance (sizing amount) from the
original edges. 2.
This technique is a very basic technique
that does not take into account special conditions such as acute angles and
may not work very well for non-fully-convex data. 3.
It may generate polygons which are
considered illegal by QisBool. 4.
It is not guaranteed that all points on
the new resized polygon are at same distance from the corresponding points on
the original polygon. 5.
This technique must only be used for
simple manhattan data. |
|
|
|
|
|
Q2. What is isotropic sizing
? |
|
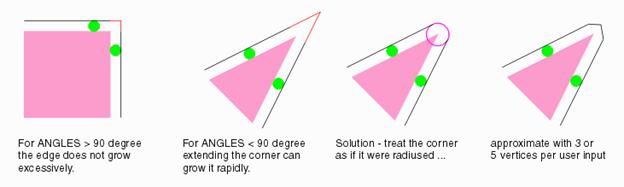
1.
Isotropic sizing is a technique that
applies a uniform sizing (along X and Y) to a polygon such that every point
on the new resized polygon is at a uniform distance from the corresponding
point on the original polygon. 2.
This is a more complex but safe-to-use
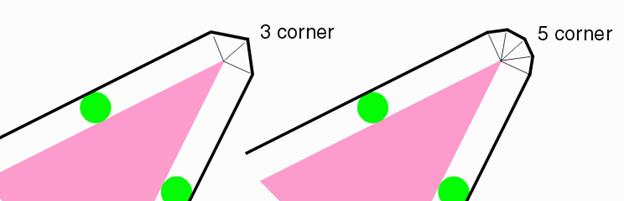
form of sizing which takes care of acute angles. 3.
This technique may result in formation of
arcs which can be broken up into either 1, 3 or 5 points. |
|
|
|
|
|
|
|
Q3. What is non-isotropic
sizing ? |
|
1.
Non isotropic sizing is similar to isotropic
sizing except that the amount of sizing in X and Y may not be the same. |
|
|
|
|
|
|
©
2012 Artwork Conversion Software Inc. |
|
|
417 Ingalls St. Santa Cruz CA 95060 |
|
|
[T] +1 831-426-6163 [F] +1 831-[E]
info@artwork.com |
|