Effect of Data Orientation on Raster Timing

One of our users was very surprised to find that his rasterization time doubled when rotating his data by 90 degrees. He assumed that the routine used to rotate the data was very inefficient. However upon further examination this proved not to be the case. The code that rotates the data (in the vector space) is very fast.

So what is the reason?

It turns out that the amount of "computational" work in rasterizing a polygon depends on how many times a horizontal scan line must be computed and the results placed in memory.

Each time the scan line crosses two polygon edges a computation is performed.


scan line across polygon 'E'


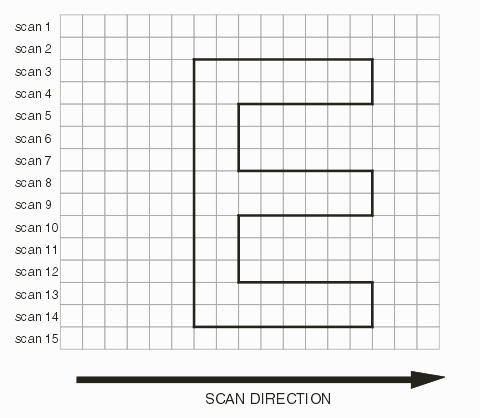
To rasterize the polygon in the illustration above, a scan line runs horziontally on each pixel row. If nothing is encountered (rows 1, 2 and 15) then no pixels need be computed or placed into memory.

Scan line 3 does encounter two edges and therefore the pixels between the two edges are computed and placed into the raster buffer. It does not matter much how "long" the run of pixels is -- about the same computational work is needed whether you are dealing with 10 pixels or 100.

So in the above illustration there are 12 scan lines where computation and memory addressing is performed.


scan line across polygon 'E' rotated 90 degrees


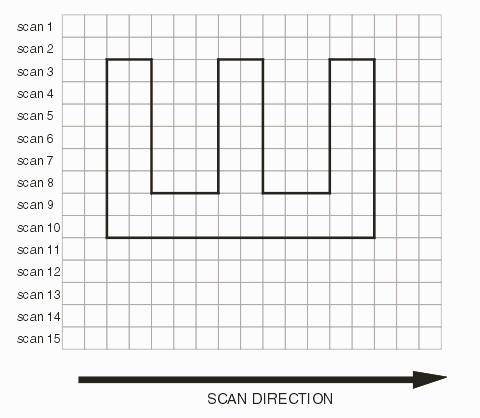
Now examine the illustration when the E shaped polygon is rotated 90 degrees.

Scan lines 3-8 each require three separate computations as they hit 3 pairs of edges. Scan lines 9 and 10 require 1 computation. The total number of raster computations is 20.

When the polygon is rotated 90 degrees there are 20 computations compared to 12 when not rotated.

Summary

Because the number of raster computations are dependent on how many polygon edges are encountered during the horizontal "scan", a particular data file's rasterization time can very greatly depending on orientation.




Note: In the interests of clarity we have made a simplification. A polygon such as the rotated E is not convex in X and would be broken down into multiple polygons that were convex in X prior to running the scan lines. However the point of additional raster computations remains true.